The Polaritonics Platform: THz Generation, Control and Detection on a Chip
Terahertz (THz) radiation is the part of the electromagnetic spectrum that lies between the infrared and microwave, and it is typically associated with frequencies between 0.1-10 THz. THz radiation is an important tool in basic science because it can be used to interrogate many THz-frequency phenomena including molecular rotations in a gas, vibrations in a molecular crystal (like sugar), and electronic transitions in nanostructures such as quantum wells or quantum dots, as well as a variety of more exotic condensed phase phenomena including Cooper pairs, polarons, and magnons.
THz frequencies lie above what is easily accessible with fast electronics and below what is easily accessible with tunable lasers, so THz technology is less advanced than in other regions of the electromagnetic spectrum. There are many challenges associated with generating and detecting THz radiation, and typically expensive ultrafast lasers are required. Guiding the THz is also difficult: wires cannot carry high enough frequencies and the beam diverges so quickly it is difficult to route the THz with optics.
The Nelson Group has developed the THz polaritonics platform to address these issues, where generation, amplification, control, and detection occur in a single compact chip. Here, the chip is a 30-100 μm thick slab of lithium niobate (LiNbO3). An intense optical pump pulse passes through the slab where it excites THz-frequency phonon-polaritons via a nonlinear optical response in the crystal. The generated THz wave is guided down the slab, where it interacts with a machined air-gap, metallic microstructure, or sample deposited on the surface (see Figure 1 below).
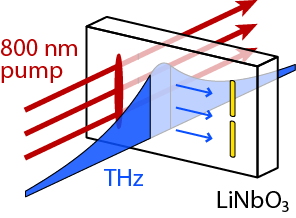
Figure 1. Polaritonics geometry. The THz is generated by an ultrafast optical pump pulse and then guided down the crystal slab, where it can interact with a sample deposited on the surface.
THz Imaging
A key capability of the polaritonics chip is the ability to image the full spatial profile of the THz electric field at each point in time as the wave propagates. We exploit the electro-optic effect in LiNbO3, where the THz electric field induces a change in the index of refraction which shifts the phase of the expanded optical probe beam used to detect the THz wave: E(x,y) ∝ Δn(x,y) ∝ Δφ(x,y).
We then use a phase sensitive imaging technique to record the induced shift, and step the time delay between pump and probe pulses to build up the full evolution of the wave. The images can be played back as a video showing interactions of the wave with structures in or on the chip, providing exceptional insight into the behavior of the integrated photonic components. Below is an example showing a THz wave diffracting off a grating.
Check out the movie theater for more movies collected using this technique!
For further information:
- C. A. Werley*, S. M. Teo*, B. K. Ofori-Okai*, P. Sivarajah, and K. A. Nelson, High-resolution, low-noise imaging in THz polaritonics, IEEE Transactions on Terahertz Science and Technology 3, 239 (2013). [url]
THz Antennas
We have used the polaritonics platform to study metal antennas deposited on the surface of the LiNbO3 slab. Pairs of half-wave antennas aligned end-to-end and separated by a small gap, like the one shown in (a) in the figure below, provide very large field enhancements in regions much smaller than the diffraction limit. We studied these antennas for three purposes: (1) to develop a component for future high-speed devices that can interconvert propagating electromagnetic waves and subwavelength electronics, (2) to harness the antenna's field enhancement to generate very high amplitude electric fields for future nonlinear THz experiments, and (3) to improve fundamental understanding of antenna behavior for experiments at all frequency ranges.
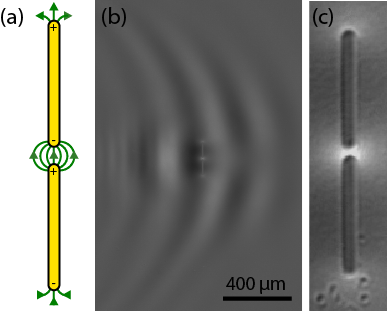
Figure 2. A THz antenna. (a) Diagram of a pair of half-wave antennas, showing field localization and enhancement at the antenna ends and in the small gap between them. (b) An image of a resonant THz wave interacting with such an antenna deposited on the surface of the lithium niobate slab. (c) A magnified view of (b) showing field localization and enhancement at the antenna ends and gap.
We used polaritonics imaging to map the THz field with λ/100 spatial resolution and fully understand the near-field profile of the antenna shown in Figures 2(b) and 2(c). We directly measured E-field enhancements up to 40-fold and developed some simple models to predict field enhancement as a function of antenna length and gap size. These insights are applicable at all frequency ranges and will aid the design of antennas for various applications including single-molecule fluorescence, surface enhanced Raman spectroscopy, near-field scanning optical microscopy. In particular, our group wants to use the extremely intense fields in the antenna gap to perform nonlinear THz spectroscopy.
For further information:
- C. A. Werley, K. Fan, A. C. Strikwerda, S. M. Teo, X. Zhang, R. D. Averitt, and K. A. Nelson, Time-resolved imaging of near-fields in THz antennas and direct quantitative measurement of field enhancement, Opt. Express 20, 8551-8567 (2012). [url]
Photonic Crystals
A photonic crystal is made of two or more materials that have different refractive indices arranged in a periodic fashion. Most commonly they are made by either cutting holes in a dielectric material or by placing rods of a dielectric in air. Because of the periodicity of the material, photonic crystals exhibit optical properties not found in normal dielectrics. The most notable new characteristic is the presence of a photonic bandgap, i.e. a range of frequencies for which light cannot propagate inside of the crystal. If light incident on a crystal has a frequency that is in the bandgap it will be rejected with very high efficiency. Figure 3 illustrates a broadband THz pulse interacting with a photonic crystal fabricated in a LiNbO3 waveguide.

Figure 3. (top) A broadband THz pulse is launched towards a photonic crystal in a LiNbO3 slab. (b) When the THz pulse reaches the photonic crystal, frequencies within the bandgap are reflected.
For further information:
- P. Sivarajah, C.A. Werley, B.K. Ofori-Okai, and K.A. Nelson, Chemically assisted femtosecond laser machining for applications in LiNbO3 and LiTaO3, Appl. Phys. A 112, 615-622 (2013). [url]
- B.K. Ofori-Okai, P. Sivarajah, C.A. Werley, S.M. Teo, K.A. Nelson, Direct experimental visualization of waves and band structure in 2D photonic crystal slabs, New J. Phys 16, 053003 (2014). [url]
Hybrid Waveguides
Hybrid waveguides composed of LiNbO3 and another material can be used to couple the THz field to other material degrees of freedom. In the hybrid waveguide shown in Figure 4(a), the THz magnetic field couples to magnons in the canted antiferromagnetic ErFeO3 to form magnon-phonon-polaritons. The magnon-phonon-polariton dispersion is shown in Figure 4(b). The avoided crossing at the magnon resonance indicates strong coupling between the phonon-polaritons in LiNbO3 and the magnons in ErFeO3.
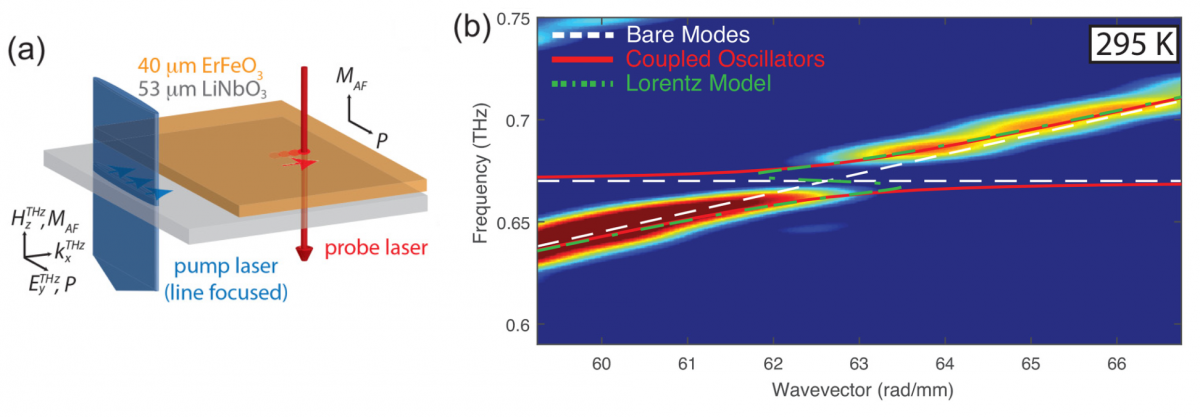
Figure 4. (a) Geometry of the hybrid waveguide structure. THz phonon-polaritons excited in LiNbO3 couple to magnons in ErFeO3. (b) Dispersion plot of the magnon-phonon polaritons. The avoided crossing at 0.67 THz indicates strong coupling between the phonon-polaritons in LiNbO3 and the magnons and ErFeO3.
For further information:
- P. Sivarajah, A. Steinbacher, B. Dastrup, J. Lu, M. Xiang, W. Ren, S. Kamba, S. Cao, K.A. Nelson, THz-frequency magnon-phonon-polaritons in the collective strong-coupling regime, J. Appl. Phys 125, 213103 (2019). [url]
Bounce Crystals
In a typical Polaritonics experiment, the generated THz field strengths are limited to 5-10 kV/cm due to the short length over which the optical pump beam interacts with the LiNbO3 crystal. While these field strengths are sufficient for linear spectroscopy, any nonlinear interactions would require far larger field strengths. Recently, we have developed a simple geometric scheme for increasing the length over which THz waves are generated. By beveling the edge of the LiNbO3 waveguide, the pump beam is refracted into the crystal and “bounces” back and forth inside. This allows the pump beam to propagate with the THz waves and continuously build up the THz amplitude.
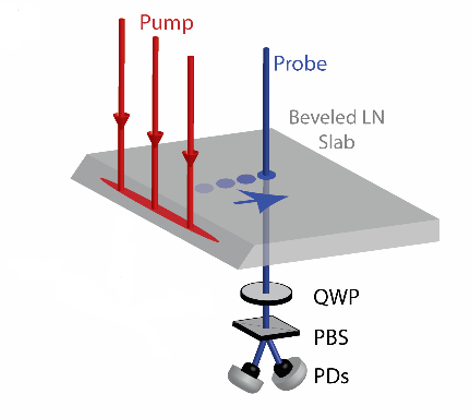
Figure 5. Geometry of a bounce crystal. The pump beam enters through the bevel and is confined inside the crystal by total internal reflection.
Check back soon for updates!
Echelon-based THz Generation
Stair-step echelon structures can be used to shape a single input Gaussian pulse into a discrete tilted pulse front composed of a sequence of “beamlets”. After the first beamlets arrives at a LiNbO3 waveguide and launched an initial THz wave, the later beamlets are timed to continually drive the same THz wave as it travels across the waveguide. This scheme leads to build up of the THz amplitude over several hundred microns.
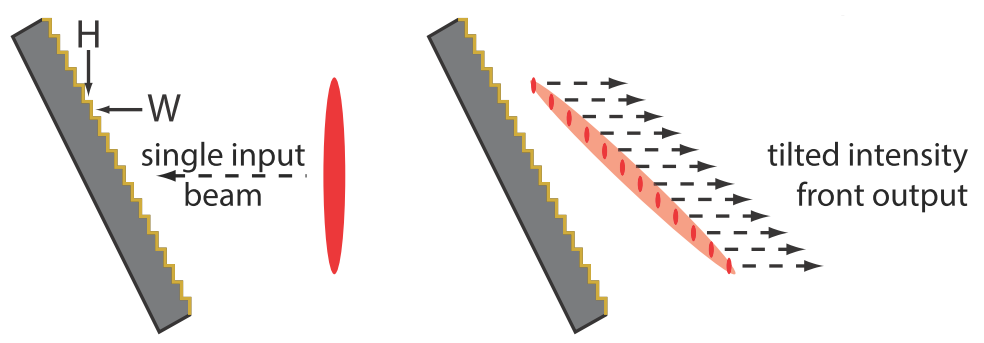
Figure 6. (left) A Gaussian input beam incident on a stair-step reflective echelon. (right) The input beam reflects off the echelon steps and is transformed into a series of beamlets that form a discrete tilted pulse front.
Check back soon for updates!
For further information:
- B.K. Ofori-Okai, P. Sivarajah, W.R. Huang, K.A. Nelson, THz generation using a reflective stair-step echelon, Opt. Express 25, 5057-5068 (2016). [url]
