To fully characterize a material’s mechanical properties, one must study their response to a range of testing conditions. The high strain and strain-rate behavior of a material is of particular importance in the understanding of nonlinear viscoelastic properties, material failure, blast mitigation, and other such extreme phenomena. In order to investigate these properties, we utilize two techniques; the Laser-Induced Particle Impact Test (LIPIT) and laser-induced shock waves.
Laser-Induced Particle Impact Testing (LIPIT)
High velocity ballistic impact phenomena range in scale from catastrophic planetary impact events, impacts related to explosives and firearms, to micron-scale additive manufacturing. Microparticle impact often poses a problem by causing erosion, but can also find use in powder blasting and cold spray manufacturing. In medicine and biology, ballistic microparticles are used for needle–free gene and drug delivery. Despite the wide range of applications, the dynamics of microparticle impact remain unexplored. While macroscale projectile impact has been studied in real time using high–speed imaging techniques, investigations of microscale impact have been limited to post–mortem analysis of impacted samples. For this purpose we have deloped an optical benchtop platform, the Laser Induced Particle Impact Test (LIPIT).
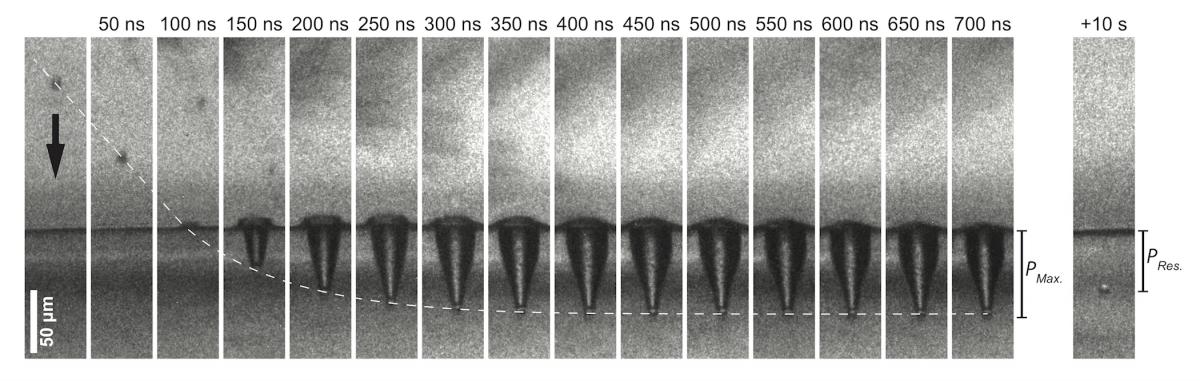
LIPIT involves focusing a high-energy laser pulse onto the back face of a “launch pad”. Launch pads consist of spherical microparticles dispersed on an elastomer-coated metallic film. Ablation of the metallic film leads to ejection of a microparticle. Microparticles are launched with speeds reaching several kilometers per second. A multi-frame high-speed camera is used to capture the impact history with nanosecond temporal and micrometer spatial resolution. The experimental tool will be capable of guiding the modeling effort and supporting the design of novel high-performance materials through direct experimental validation.
Review paper: Veysset, David, et al. "High-velocity micro-projectile impact testing." Applied Physics Reviews 8.1 (2021): 011319.
Fig. (i) Schematic representation of LIPIT. A picosecond laser pulse is focused on a launching pad on top of which micro-particles are deposited. Particles are accelerated upon laser ablation to supersonic speed (3 km/s). (a) Multi–frame sequences with 5 ns exposure time showing single–projectile impacts on (a) a protein-base hydrogel, (b) a poly(urethane urea) (PUU) elastomer, and (c) an aluminum substrate. (a) Impact of a silica sphere (7.4 um diameter) at 500 m/s followed by projectile penetration. (b) Impact of a silica sphere (7.4 um diameter) on PUU at 670 m/s followed by projectile rebound. (c) Impact of a aluminum particle (40 um diameter) at 800 m/s followed by particle adhesion.
Laser-induced shock wave studies
Shocks are stress waves associated with high-pressures and high-strain rates, characterized by a discontinuous jump in state variables across the “shock front”. Shock loading is associated with strain rates on the order of 106 to 109 s-1 and stresses exceeding several gigapascals. The study of shock waves is of importance in understanding the effects of extreme phenomena, including blast-waves from explosive materials and primary traumatic brain injury as well as in the generation of exotic states of matter through strain.
Our laser-induced shock wave platform serves as a benchtop, all-optical technique for the study of shock wave induced phenomena. The technique involves focusing of high-energy laser pulses onto thin material layers (<100 μm) sandwiched between two glass slides. Absorption of the laser energy leads to rapid thermal expansion that generates a shock wave traveling laterally in the plane of the sample. Pressures are varied by tuning the input laser energy, with pressures of up to tens of gigapascals readily achieved. To date, this technique has been used to study high pressure generation in liquids and solids, pressure induced fracture and phase transitions, acoustic wave induced cell permeability for drug delivery, as well as shock induced cavitation in soft materials.
Fig. (left) Cartoon representation of the laser induced shock wave technique. High energy pump pulses focused onto samples launch shock waves in the plane of the sample via rapid thermal expansion. Samples consist of thin layers of material sandwiched between two substrates. (right) laser-induced shock wave in water, probed by femtosecond imaging. The dark region on the left hand side is the laser-excitation region. In this image, the excitation pulse was focused to a line, launching a planar shock wave traveling towars the right.
The lab is located in NE47-580.
see below for more experimental details. Representative publications listed at bottom of page.
Fig. (a) Coefficient of restitution for impacts of copper particles on a copper substrate with SEM images corresponding to impacts at (b) 400 m/s, where rebound occurs with no apparent signs of jetting; (c) 550 m/s, where rebound occurs with signs of incipient jetting observed on the substrate; and (d) 770 m/s, where bonding occurs and jetting is observed originating from both the particle and substrate. The scale bar is 5 μm. (Sun et. al. J. App. Mech. 2020).
In collaboration with Prof. Carlos Portela (Dept. Mechanical Engineering, MIT), impacts on microarchitected materials have been conducted. LIPIT experiments have been used to characterize the specific inelastic energy absorption of these materials, revealing their impact resistance to be superior to that of Kevlar composites and nanoscale polystyrene films. It was discovered that propagation of compaction shock waves serve as a mechanism for efficient energy dissipation in these materials.
Fig. impact processes and resulting damage. a,b, Impact onto nanoarchitected carbon materials of ~23% relative density with impact and rebound velocities of 238 and 50 m s−1, respectively (a), and impact velocity of 676 m s−1 and particle capture (b). c, Sample of ~23% relative density after elastic impact with no permanent deformation at 50 m s−1. d,e, Post-impact micrographs of sample from a showing cratering (d) and sample from b showing a captured SiO2 particle (e). White scale bars, 20 μm; black inset scale bars, 5 μm. (Portela et. al. 2021).
Converging shock waves benefit from amplification of pressure as the shock approaches the focus. Using an axicon to focuses an intense picosecond excitation pulse into a ring-shaped pattern, we are able to excite converging shock waves (see below). Use of converging shock waves allows us to readily produce pressures on the order of tens of gigapascals.
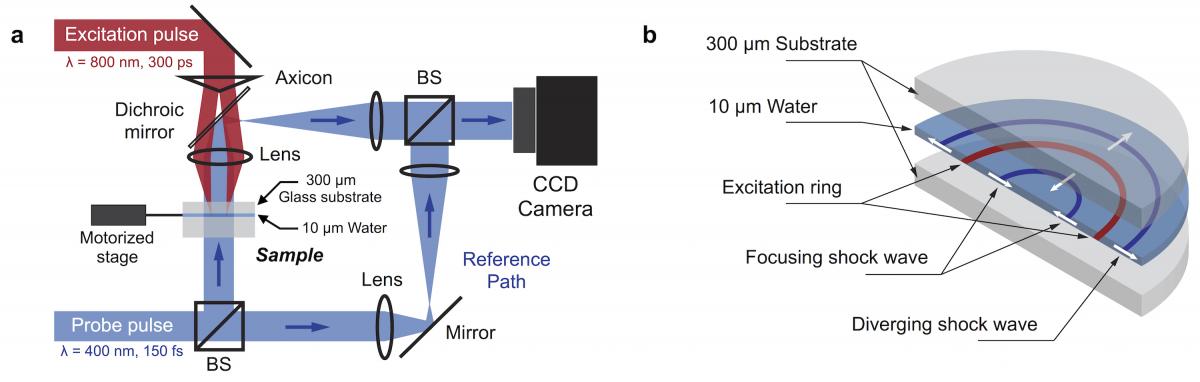
Fig. (a) Excitation pulse is focused into a ring in the plane of the water layer using an axicon-lens configuration. Interferometric imaging is performed in the Mach-Zehnder configuration using a variably delayed probe pulse. (b) Cutaway-view representation of the sample. After laser absorption by the carbon nano-particles, two counter-propagating shock waves are launched and remain confined in the plane of the sample.
Using a Mach-Zehnder interferometer and time-delayed femtosecond laser pulses, we obtain a series of images tracing the shock wave as it converges at the center of the ring before reemerging as a diverging shock. Through quantitative analysis of the interferograms, density profiles of shocked samples are extracted (see below, left). The experimental geometry used in our study opens prospects for spatially resolved spectroscopic studies of materials under shock compression. In liquids and polymeric materials we have observed cavitation induced by converging shock waves (see below).
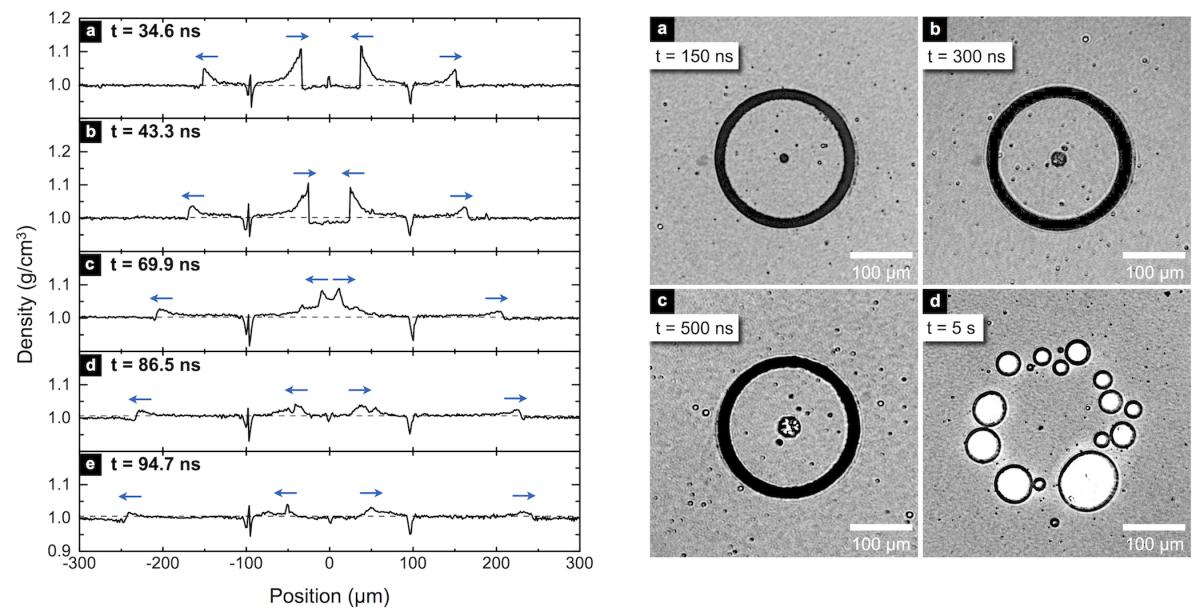
Fig. (left) Water density profiles extracted along a ring diameter for five delays between the excitation pulse and the probe pulse: 34.6 ns, 43.3 ns, 69.9 ns, 86.5 ns, and 94.7 ns. Rapid density jumps indicate shock fronts, with the arrows showing the propagation direction. The horizontal dashed line marks the undisturbed density of water at room temperature. The density drop at x = ± 95 µm is caused by bubble formation at the excitation ring location (a-e). A density dip at the center in (d-e) and (i-j) indicates the formation of a cavitation bubble. (right) Non-interferometric images recorded (a) at 150 ns, (b) 300 ns, (c) 500 ns and (d) at 5 s delay showing bubble cavitation following shock focusing. (Veysset et. al. Sci. Rep. 2016)
Fig. (left) Displacement profile caused by converging surface acoustic wave (SAW) on strontium titanate. (center) interferometric image. (left) fracture at center of excitation region caused by converging SAW. The scale bar is 50 μm
We are currently working towards introducing spectroscopic probes for studying not only shock wave propagation but also the material evolution under shock, including phase transitions, chemical reactions, and other shock-assisted effects.
For more details regarding LIPIT experiments see:
Lee, Jae-Hwang, et al. "High strain rate deformation of layered nanocomposites." Nature communications 3.1 (2012)
Veysset, David, et al. "Dynamics of supersonic microparticle impact on elastomers revealed by real–time multi–frame imaging." Scientific reports 6.1 (2016): 1-6.
Veysset, David, et al. "Molecular influence in high-strain-rate microparticle impact response of poly (urethane urea) elastomers." Polymer 123 (2017): 30-38.
Hassani-Gangaraj, Mostafa, et al. "Melting can hinder impact-induced adhesion." Physical review letters 119.17 (2017): 175701.
Hassani-Gangaraj, Mostafa, et al. "In-situ observations of single micro-particle impact bonding." Scripta Materialia 145 (2018): 9-13.
Veysset, David, et al. "High-velocity micro-particle impact on gelatin and synthetic hydrogel." Journal of the mechanical behavior of biomedical materials 86 (2018): 71-76.micro-particle impact on gelatin and synthetic hydrogel. J. Mech. Behav. Biomed. Mater. 86, 71–76.
Sun, Yuchen, et al. "Molecular dependencies of dynamic stiffening and strengthening through high strain rate microparticle impact of polyurethane and polyurea elastomers." Applied Physics Letters 115.9 (2019): 093701.
Portela, Carlos M., et al. "Supersonic impact resilience of nanoarchitected carbon." Nature Materials 20.11 (2021): 1491-1497.
More details regarding shock focusing can be found in:
Pezeril T, Saini G, Veysset D, Kooi S, Fidkowski P, et al. 2011. Direct visualization of laser-driven focusing shock waves. Phys. Rev. Lett. 106(21):2145031.
Veysset D, Pezeril T, Kooi S, Bulou A, Nelson KA. 2015. Laser-induced versus shock wave induced transformation of highly ordered pyrolytic graphite. Appl. Phys. Lett. 106(16):161902
Veysset D, Мaznev AA, Pezeril T, Kooi S, Nelson KA. 2016. Interferometric analysis of laser-driven cylindrically focusing shock waves in a thin liquid layer. Sci. Rep. 6(1):24
Veysset, D., Kooi, S.E., Haferssas, R., Hassani-gangaraj, M., Islam, M., Maznev, A.A., Chernukha, Y., Zhao, X., Nakagawa, K., Martynowych, D., Zhang, X., Lomonosov, A.M., Schuh, C.A., Radovitzky, R., Pezeril, T., Nelson, K.A. Glass fracture by focusing of laser-generated nanosecond surface acoustic waves. Scr. Mater. 158, 42–45. (2019)
Dresselhaus-Cooper, Leora, et al. "Single-shot multi-frame imaging of cylindrical shock waves in a multi-layered assembly." Scientific reports 9.1 (2019): 1-12.
Ito, Yusuke, et al. "Interferometric and fluorescence analysis of shock wave effects on cell membrane." Communications Physics 3.1 (2020): 1-6.
Dresselhaus-Cooper, Leora E., et al. "Pressure-Thresholded Response in Cylindrically Shocked Cyclotrimethylene Trinitramine (RDX)." The Journal of Physical Chemistry A 124.17 (2020): 3301-3313.
Pereira, Diogo A., et al. "Imaging of photoacoustic-mediated permeabilization of giant unilamellar vesicles (GUVs)." Scientific reports 11.1 (2021): 1-12.
Research Update: https://nelson.mit.edu/news/high-velocity-micro-particle-impact-gelatin-...">High-velocity micro-particle impact on gelatin and synthetic hydrogel